Research

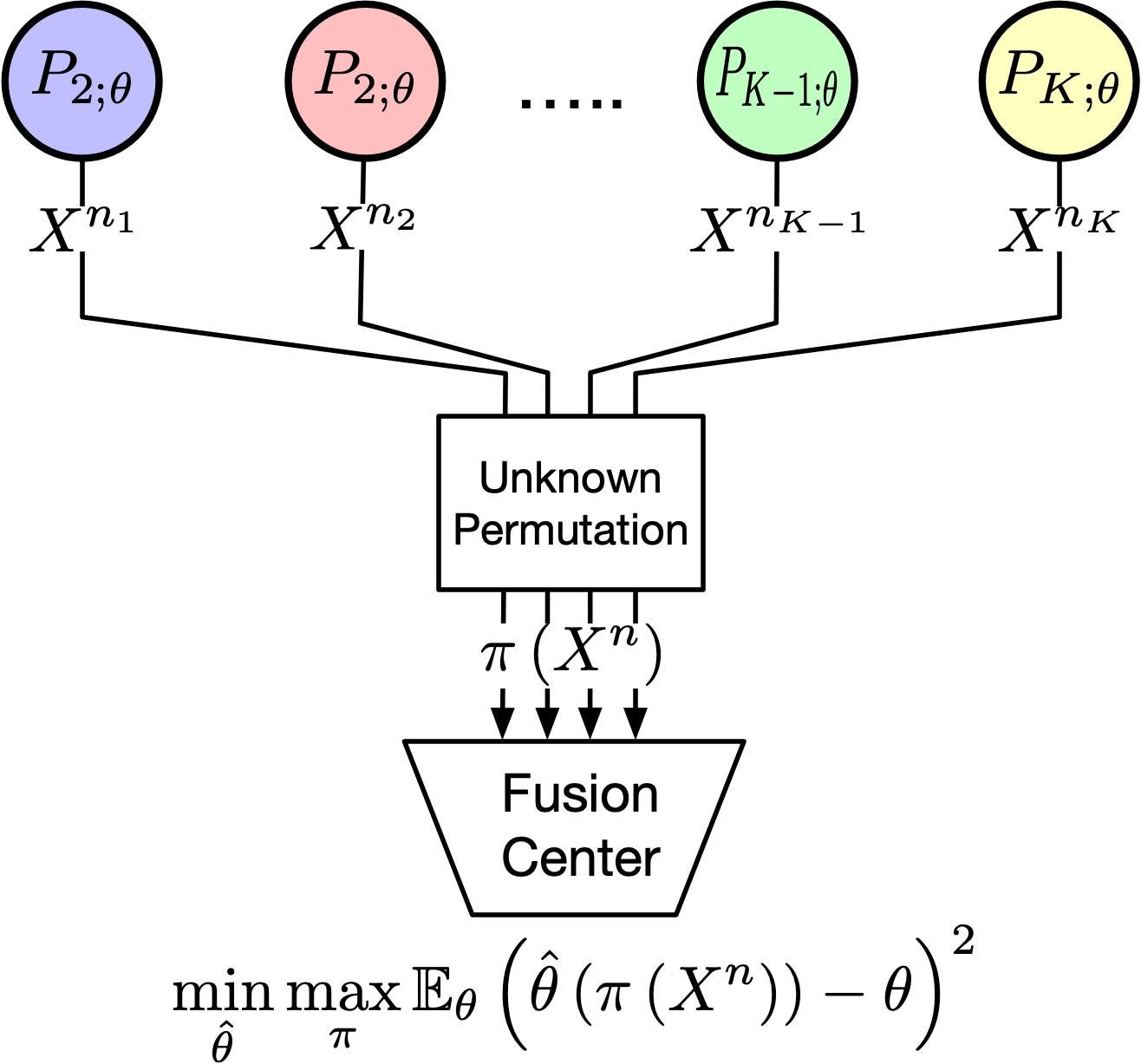
Consider the problem of anonymous parameter estimation with $n$ samples drawn from $K$ independent but non-identical sources. The key challenge is the anonymity of samples -- they are passed through an unknown permutation $\pi$ before the fusion center observing them, making identifying the underlying distribution of individual sample difficult. We aim to find an estimator which minimizes the worst-case (possible permutation) mean square error (MSE) and to specify the asymptotic Fisher information as $n$ tends to infinity, assuming the number of samples from each source is proportional to $n$. Our results are two-fold: we showed that the optimal estimator depends only on the empirical distribution of samples, and we also explicitly characterized how anonymity decreases the Fisher information.

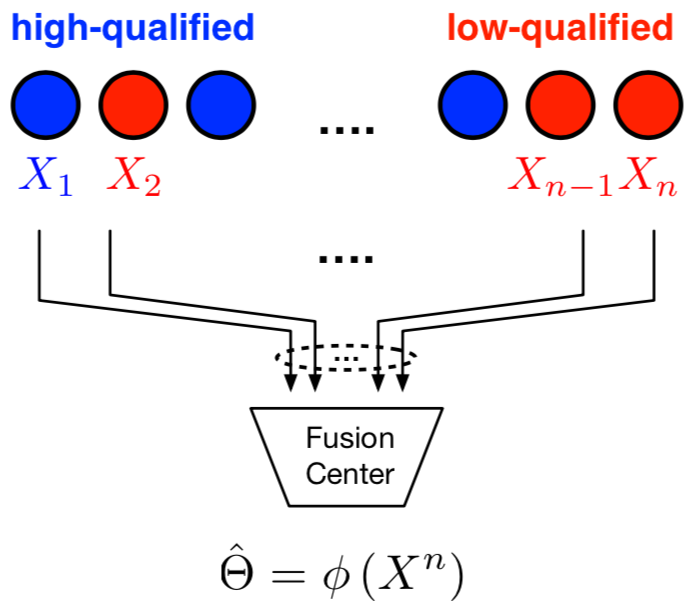
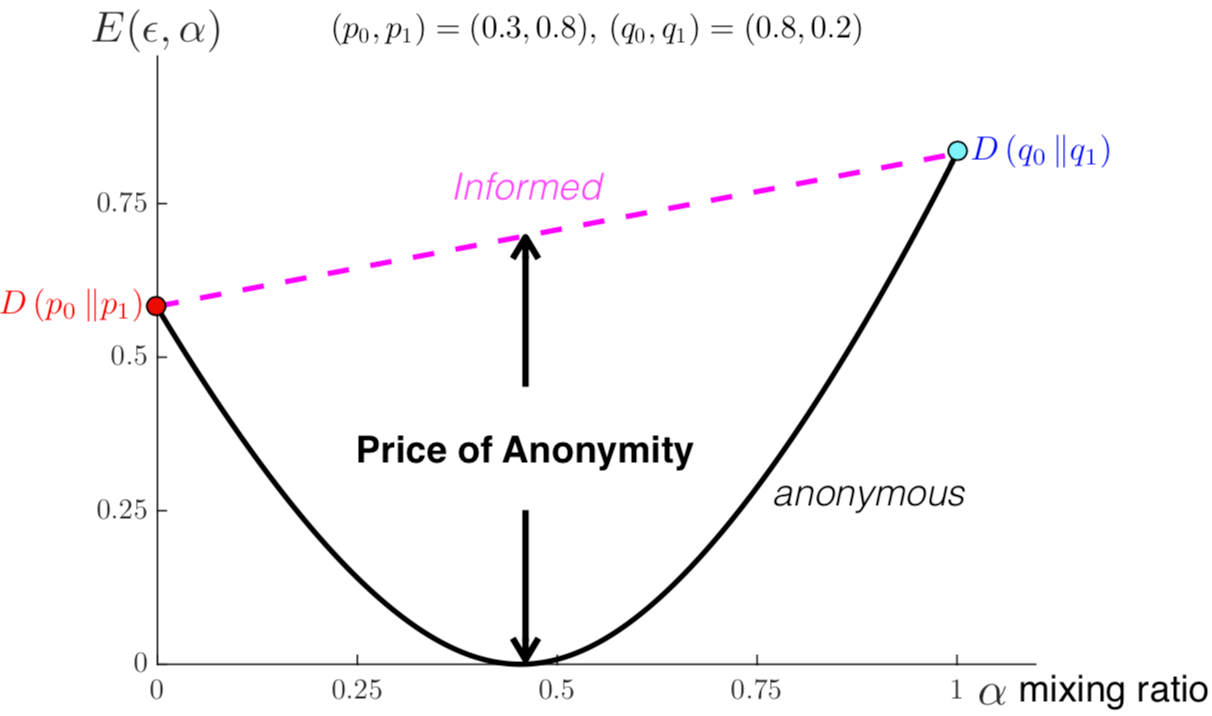
We explore the fundamental limits of heterogeneous distributed detection in an anonymous sensor network with $n$ sensors and a single fusion center. The fusion center collects the single observation from each of the $n$ sensors to detect a binary parameter. The sensors are clustered into multiple groups, and different groups follow different distributions under a given hypothesis. The key challenge for the fusion center is the anonymity of sensors -- although it knows the exact number of sensors and the distribution of observations in each group, it does not know which group each sensor belongs to. It is hence natural to consider it as a composite hypothesis testing problem. Our results elucidate the price of anonymity in heterogeneous distributed detection, and can be extended to M-ary hypothesis testing with heterogeneous observations generated according to hidden latent variables. The results are also applied to distributed detection under Byzantine attacks, which hints that the conventional approach based on simple hypothesis testing might be too pessimistic.

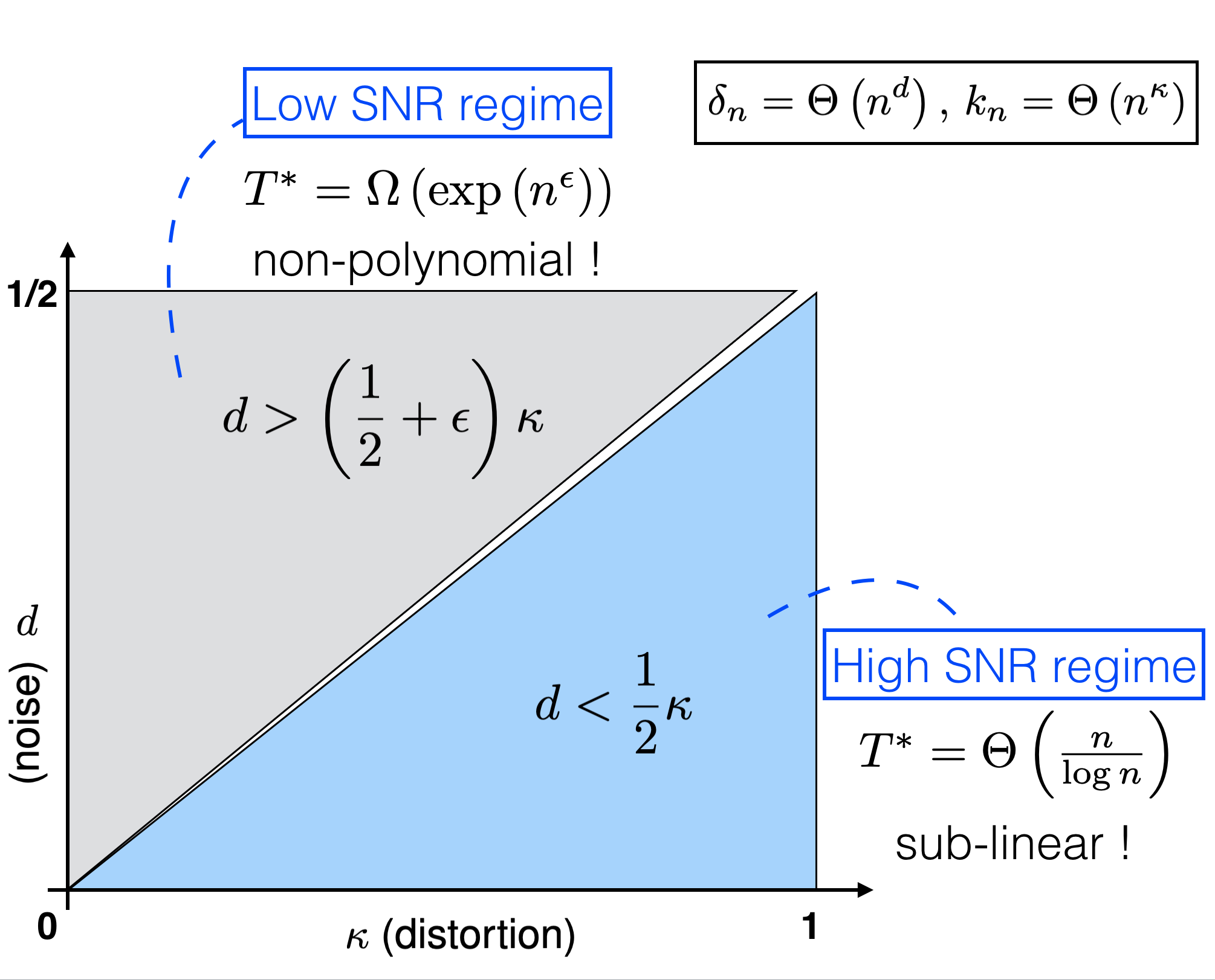
The considered data set is a collection of $n$ items, each of which carries a piece of categorical data taking values in a finite alphabet. Data analysts are allowed to query the data set through a curator by specifying a subset of items and then obtaining the histogram of the queried subset. The (unnormalized) histogram released by the curator, however, is perturbed by some additive noise with maximum magnitude $\delta_n$. The goal of the data analyst is to reconstruct the categorical data set such that the Hamming distance between the reconstructed and the actual one is smaller than a tolerance parameter $k_n$. In this work, we explore the fundamental limit on the minimum number of queries $T_n^*$ required for the analyst to reconstruct the $n$-item data set within $k_n$ tolerance subject to $\delta_n$ noisy perturbation. We first show that if $\delta_n = O(\sqrt{k_n})$, the minimum query complexity $T^*_n = \Theta(n/\log n)$, where the achievability is based on random sampling, and the converse is based on counting and packing arguments. On the other hand, if $\delta_n = \Omega( k_n^{(1+\epsilon)/2})$ for some $\epsilon > 0$, we prove that $T_n^* = \omega(n^p)$ for any positive integer $p$. In other words, no querying methods with polynomial-in-$n$ query complexity can successfully reconstruct the data set in that regime. This impossibility result is established by a novel combinatorial lower bound on $T_n^*$.

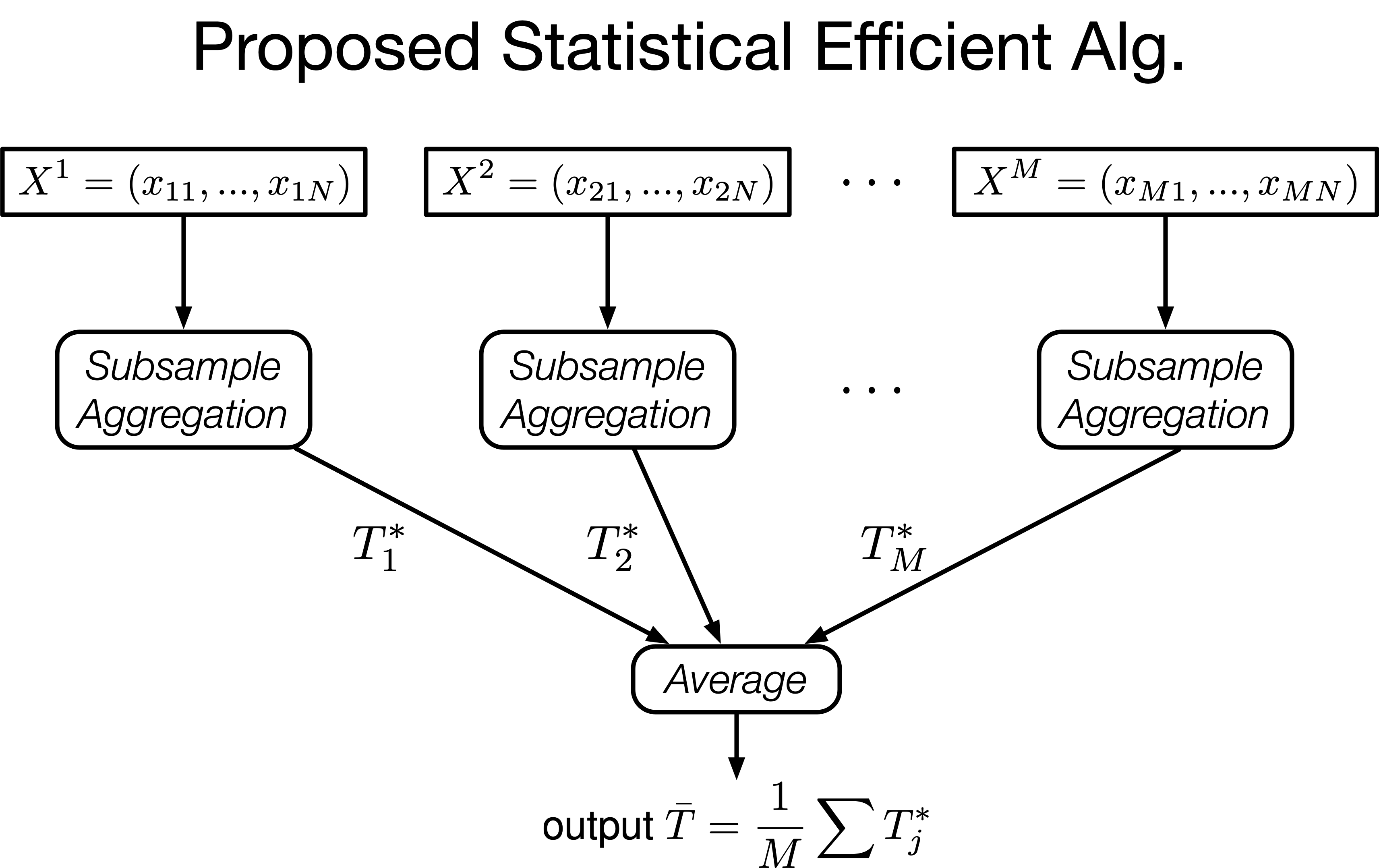
Consider the problem of parameter estimation with data collected from $M$ parties, each party holding $N$ copies of identically and independently distributed (i.i.d.) samples. In many circumstances, parties are not willing to reveal their private information, so the released data will be $\epsilon$-differential private. In this paper, we propose two algorithms to estimate parameter: for general dataset with the number of samples satisfying $M = o\left( N^2\right)$ and the privacy parameter satisfying $\epsilon=\Omega\left( N^{1/6}M^{-1/3}\right)$, we proposed subsample-and-aggregate estimator, which is asymptotically efficient (i.e. its MSE is asymptotically equal to Fisher information). On the other hand, if the underlying distributions are from exponential family and if $\epsilon=\Omega\left( 1/N\right)$, we showed that sufficient-statistic-averaging is always efficient as $N$ goes to infinity. Our results showed that as long as the number of parties does not grow too fast, one can guarantee differential privacy for free, without sacrificing the performance of estimation.